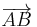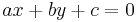Direction vector
In mathematics, a direction vector that describes a line segment D is any vector
where  and
and  are two distinct points on the line D. If v is a direction vector for D, so is kv for any nonzero scalar k; and these are in fact all of the direction vectors for the line D. Under some definitions, the direction vector is required to be a unit vector, in which case each line has exactly two direction vectors, which are negatives of each other (equal in magnitude, opposite in direction).
are two distinct points on the line D. If v is a direction vector for D, so is kv for any nonzero scalar k; and these are in fact all of the direction vectors for the line D. Under some definitions, the direction vector is required to be a unit vector, in which case each line has exactly two direction vectors, which are negatives of each other (equal in magnitude, opposite in direction).
Contents |
Direction vector for a line in R2
Any line in two-dimensional Euclidean space can be described as the set of solutions to an equation of the form
where a, b, c are real numbers. Then one direction vector of 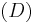 is
is 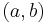 . Any multiple of
. Any multiple of 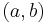 is also a direction vector.
is also a direction vector.
For example, suppose the equation of a line is 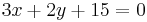 . Then
. Then 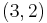 ,
, 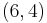 , and
, and 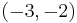 are all direction vectors for this line.
are all direction vectors for this line.
Parametric equation for a line
In Euclidean space (any number of dimensions), given a point a and a nonzero vector v, a line is defined parametrically by (a+tv), where the parameter t varies between -∞ and +∞. This line has v as a direction vector.
See also
External links
- Weisstein, Eric W. "Direction." From MathWorld--A Wolfram Web Resource. [1]
- Glossary, Nipissing University
- Finding the vector equation of a line
- Lines in a plane - Orthogonality, Distances, MATH-tutorial
- Coordinate Systems, Points, Lines and Planes